数学で使われる「数学記号」とは。覚えておきたい記号とその意味を紹介

数学では、いろいろな概念を記述する際に記号を使って式を書き表します。このように、数学上に抽象化された概念を簡潔に表すための記号を「数学記号」と呼びます。

電気工事士、電気主任技術者試験など、電気に関する資格試験を受ける場合、この「数学記号」について知っておく必要があります。

この記事では、数学記号とその意味、さらに電気工事士・電気主任技術者試験ではどのように問題が出題されるのかをご紹介します。

数学で使われる記号とその意味

数学で使われる記号は「数学記号」と呼ばれ、数式を書き表すときに用いられます。＋、―、×、÷以外にも、様々な記号があり、それぞれが意味を持っています。　※記号のヨコの「▼」をクリックすると、本記事内の解説部分へジャンプします。

	記号	意味	使い方の例	（　）は読み方
▼	＝	イコール、等しい	\(a\)は\(b\)に等しい	\(a=b\)（\(a\)イコール\(b\)）
▼	≠	ノットイコール、等しくない	\(a\)は\(b\)に等しくない	\(a≠b\)（\(a\)ノットイコール\(b\)）
▼	≒	ほぼ等しい、ニアリイコール	\(\displaystyle \frac{1}{6}\)は0.167にほぼ等しい	\(\displaystyle \frac{1}{6}≒0.167\)
▼	≡	合同、恒等
▼	＋	プラス、加える、足す	\(a\)に\(b\)を足す	\(a+b\)
▼	ー	マイナス、引く	\(a\)から\(b\)を引く	\(a-b\)
▼	×，・	掛ける	5に3を掛ける \(a\)に\(b\)を掛ける （記号のときは・を省略可）	\(5×3\) \(a×b\)，\(a・b\)，\(ab\)
▼	÷，/	割る	3を5で割る \(a\)を\(b\)で割る	\(3÷5\)，\(\displaystyle \frac{3}{5}\) \(a÷b\)，\(\displaystyle \frac{a}{b}\)
	～	差	\(a\)と\(b\)の差 （大きい方から小さい方を引く）	\(a～b\)
▼	＜	より小さい	\(a\)は\(b\)より小さい	\(a＜b\)（\(a\)小なり\(b\)）
▼	＞	より大きい	\(a\)は\(b\)より大きい	\(a＞b\)（\(a\)大なり\(b\)）
▼	≦	より小さいか等しい	\(a\)は\(b\)より小さいかあるいは等しい	\(a≧b\)（\(a\)小なりイコール\(b\)）
▼	≧	より大きいか等しい	\(a\)は\(b\)より大きいかあるいは等しい	\(a≦b\)（\(a\)大なりイコール\(b\)）
▼	≪	より非常に小さい	\(a\)は\(b\)より非常に小さい	\(a≪b\)
▼	≫	より非常に大きい	\(a\)は\(b\)より非常に大きい	\(a≫b\)
▼	∞	無限大
▼	∝	比例する	電流\(I\)は電圧\(V\)に比例する	\(I\)∝\(V\)
▼	∽	相似		\(\mathrm{\,△ABC}\)∽\(\mathrm{\,△DEF}\)）
▼	：	比	\(a\)と\(b\)の比	\(a:b\)（\(a\)たい\(b\)，\(a\)対\(b\)）
▼	∴	ゆえに		\(V=IR\) ∴\(I=\displaystyle \frac{V}{R}\)
▼	∵	なんとならば なぜならば	\(a\)と\(c\)は等しい なんとなれば\(a=b\)、\(b=c\)であるから	\(a=c\) ∵\(a=b,b=C\)
▼	⊥	垂直	直線\(\mathrm{\,AB}\)と直線\(\mathrm{\,CD}\)は垂直	\(\overline{\mathrm{\,AB}}⊥\overline{\mathrm{\,CD}}\)
▼	//	平行	直線\(\mathrm{\,AB}\)と直線\(\mathrm{\,CD}\)は平行	\(\overline{\mathrm{\,AB}}//\overline{\mathrm{\,CD}}\)
	Σ	シグマ、総和	1点に集まる電流\(i\)の総和は0
▼	| |	絶対値	-5の絶対値は5	\(|-5| = 5\) （-5の絶対値イコール5）

等号の記号

とっても当たり前なのですが、「同じだよ」ということを示す「等号」の記号が必要です。数学とは、同値関係の数だけ分野がある、と呼ばれるほど、「同じもの」を見つけ続ける学問です。計算の値は同じ、方程式の解は同じ、図形は合同、、、それらをどんどん抽象化して、一般的に成立する美しいものを見つけるのが数学という学問のようです。電気の世界では、その恩恵を使わせていただいています。

まずは手始めに、「＝」という記号を紹介します。これは、左右に書かれたものが同じであることを示す記号です。「＝」の定義は「\(A＝A\)」を満たすということです。左右に書かれたものが異なるものの場合は「≠」記号を用いて「\(A≠B\)」などと表現します。

そして、数学では、次のことを前提（公理）として、実り豊かな恩恵を与えてくれています。　

「同じものに等しいものは、互いに等しい」

つまり、「\(A=B\) で \(B=C\) ならば、 \(A=C\) 」
前提条件（公理）から出発して、
\(a\) だから \(b\)　\(∴ b\) だから \(c\)　\(∴ c\) だから \(d\)　∴・・・
と、この論理を何度も何度も繰り返していきます。「∴」は、「ゆえに」という意味です。

公理から導かれるすべての結果は、その強固な論理に支えられているというのが数学の強みです。それを記述するためにも様々な数学記号が定義されています。

ここで数学記号の厳密な定義を述べることは無理ですが、たまには「使う」だけでなく、その中身に触れてみるのもよいでしょう。本稿では、数学記号の意味を、少しだけですが解説していきます。

四則演算の記号

四則演算の記号とは、加減乗除、すなわち足し算・引き算・掛け算・割り算を表す記号「＋」「－」「×」「÷」です。掛け算は「・」、割り算は「／」や分数が用いられる場合も多いです。これらは、すべての計算問題の基本となる記号です。

加法（足し算）

交換法則

足し算の順序を入れ換えても結果は変わらない

　　\(A+B=B+A\)

結合法則

どこから足し算しても結果は変わらない

　　\( (A+B)+C=A+(B+C)=A+B+C\)

単位元の存在

0を加えても変わらない（足し算の出発点がある）

　　\(A+0=A\)

逆元の存在

大きさ（絶対値）が同じで異符号の数との和は0

　　\(A+(-A)=0\)

減法（引き算）

引き算は、マイナス（逆元）の足し算で定義されます。

　　\(A-B=A+(-B)\)

このことから、交換法則や結合法則が成立しません。

例えば、\(A-B\)を入れ替えた \(B-A\)は

　　\(A-B≠B-A\)

となりますね。

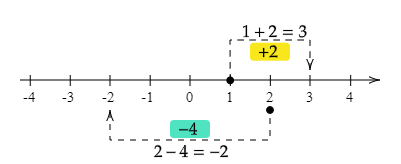
ここで、足し算や引き算のイメージを絵にすると、図１のようになります。足し算は数直線上の値を右へ（大きい方へ）、引き算は左へ（小さい方へ）移動させる演算です。

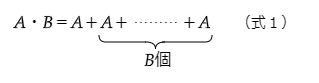
乗法（掛け算）

掛け算は、足し算を繰り返し行うことで定義されます。

なお、数字同士の掛け算の場合、小学校では「\(2×3＝6\)」のように、クロス記号「×」を使うと習います。しかし、中学校になると、文字式の計算では「\(24y\)」のようにクロス記号「×」を省略したり、「2・x 」のようにミドルドット記号「・」を使うと習います。

掛け算される量がスカラー量（大きさのみを持ったもの。実数が典型的な量。）の場合は「×」でも「・」でも同じ意味と捉えることができるので問題ありません。しかし、ベクトル量（向きと大きさを持った量。フェーザも含まれる）の掛け算では、「×」はクロス積（外積の特殊な場合）、「・」は内積という異なる掛け算を意味します。

ですから、文字式を取り扱うようになると「×」は紛らわしいので使わないほうがよいのです。ところが、数字を表記するとなると、「・」記号と小数点のコンマが区別しずらいため、「×」も利用されます。

掛け算の定義から、次の性質が得られます。

交換法則

掛け算の順序を入れ換えても結果は変わらない

　　\(A・B=B・A\)

結合法則

どこから掛け算しても結果は変わらない

　　\((A・B)・C=A・(B・C)=A・B・C\)

分配法則

また、足し算と掛け算の性質を合わせて

　　\(A・(B+C)=A・B+A・C\)

が得られます。

除法（割り算）

割り算は、掛け算の逆として定義できます。

　　\(A÷B=C\)

とは、

　　\(A=B×C(=C×B)\)

を満たすCを求める計算をすることになります。

Aを割られる数（被除数）、Bを割る数（除数）、Cを商といいます。
\(B=0\) の場合は、\(0×C=C×0=0\)ですから、これを満たすようなCなど存在せず、割り算は定義できません。

割り算は、分数を用いて

　　\(\displaystyle\frac{A}{B}=C\)　（式２）

とも表記されます。割り算は、逆数の掛け算として、

　　\(\displaystyle\frac{A}{B}=A×\frac{1}{B}\)　（式３）

とも計算できます。

当然、

　　\(A÷B≠B÷A\)

ですから、交換法則は成り立ちません。

一方、割る数（除数）に対しては結合法則が成立し、割られる数（被除数）に対しては結合法則は成立しません。

つまり、

　　\((A+B)÷C=A÷C+B÷C\)　（式４）

は成立しますが、

　　\(\displaystyle\frac{A+B}{C}=\frac{A}{C}+\frac{B}{C}\)　（式５）

は成立しません。多くの方が（式５）は不成立にも拘らず、やってしまっているケースをよく見受けます。

割り算では、分数は逆数の掛け算で表されることから、次のことがいえます。

　　\(A ÷ ( B ÷ C ) = A × ( C ÷ B ) = (A × C) ÷ B\)

分数では

　　\(\displaystyle\cfrac{A}{\cfrac{B}{C}}=A÷\cfrac{B}{C}＝A×\cfrac{C}{B}=\cfrac{AC}{B}\)　（式７）

となります。なお、等号「＝」の横に位置する分数線が割り算の位置を示しています。（式７）では \(A\) と\(( B ÷ C )\)の間に「＝」がありますね。

一方、

　　\(\displaystyle\cfrac{\cfrac{A}{B}}{C}=\cfrac{A}{B}÷C=\cfrac{A}{BC}\)　（式８）

は、 \((A÷B)\) と \(C\) の間に「＝」が位置する分数線がありますから、（式７）と（式８）で結果は異なります。

四則計算のルール

四則計算は次の順に行います。

べき乗は、掛け算を繰り返す演算で、記号はないのですが、指数を用いて

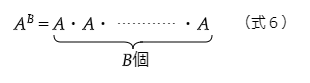
と掛け算を繰り返す演算です。

なお、日本の場合、カッコ記号は
大カッコ[ ]　→　中カッコ { }　→小カッコ ( )
の順に [ { ( ) } ] と利用されます。

例： \(3^2 × (3 + 1) + 5\)　を計算する流れ

先に紹介した、足し算や掛け算で成立する交換法則を適用して、答えが変わらないことを確かめてみましょう。また、掛け算については分配法則が成立することも確かめてみましょう。

代数学の記号

代数学とは、数の代わりに文字を使って方程式の解き方などを研究する学問のことです。

代数学で使用する記号を紹介する前に、まずは数の四則計算に対する性質を確認していきましょう。

自然数

自然数は１、２、３、４、・・・と、基準の数から１つずつ数をカウントしてできる数のことです。０を含める流儀と含めない流儀がありますが、いずれにしても次の性質が成立します。

小さい自然数から大きい自然数を引き算するなどすると、負の数になってしまいます。そこで、整数を

・・・、ー３、ー２、ー１、０、１、２、３、・・・

のように、いくら引き算を実行しても大丈夫なように導入します。また、割り算に対しては、整数の比で表されるものを有理数と定義します。すると、次のような性質が得られます。

ここまで確認すると、有理数同士で四則計算を行っても、その結果は有理数になることがわかります。このような性質を「体」といいます。

これで全ての数が表現できたかというと、そんなことはありません。１辺の長さが１の正方形の対角線の流さは\(\sqrt{2} = 1.4142・・・\)といった、整数の比では表されない数があります。そこで、数直線上のあらゆる数のことを実数と呼びます。実数も「体」となり、

という性質があります。また、\(\sqrt{2} \)や円周率\(π\)のように、有理数でない実数を無理数といいます。無理数も実数なので、当然「体」となります。一応書いておくと、

ですね。

さて、図２のように、実数を表現する数直線を２本用意して直交させます。横軸の数直線上の＋１にー１を掛けると、180°反転してー１の位置に現れます。では、半回転した位置を表すにはどうすればよいか。ある数\(j\)をかけると90°回転するとしましょう。そして、＋１から\(j\)を２回かけて、２回90°回転させます。すると180°回転して-1の位置になりますから、

　　\((+1)・\mathrm{\,j}・\mathrm{\,j} = -1\)

となります。つまり

　　\(\mathrm{\,j}^2 = -1  , \mathrm{\,j} = \sqrt{-1}\)

となるのです。

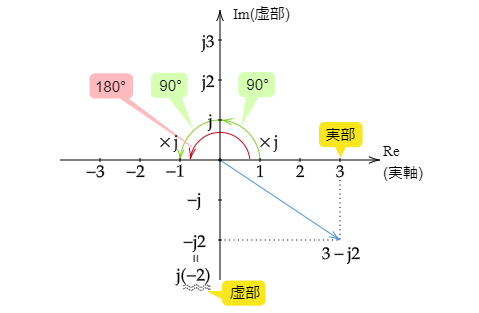
このように、直交する２つの数直線によって平面をつくるとき、90°の回転をさせるような基本単位 \(\mathrm{\,j} = \sqrt{-1}\)　を虚数単位といいます。数学ではimaginary numberの頭文字\(i\)を用いますが、電気の世界では\(i\)は電流の瞬時値と被るため、アルファベットが隣の\(j\)が用いられます。

そして、２つの実数a, bを用いて

　　\(a + \mathrm{\,j}b\)

と表現される数を複素数といいます。２つの複素数 \(a + \mathrm{\,j}b\) と \(c + \mathrm{\,j}d\)が等しい、すなわち

\(a + \mathrm{\,j} b = c + \mathrm{\,j}d \) とは、それぞれの実部と虚部が等しい\( a = c\) かつ \(b = d\) と定義します。

また、複素数も「体」になります。

複素数が体となる性質は、どの参考書でも確認できますので、交流理論を勉強する際には必ず確認しておきましょう。

複素共役

複素数の虚部の正負を入れ替えたものを複素共役といいます。\(a +\mathrm{\,j}b\) の複素共役は \(a – \mathrm{\,j}b\)です。数式では、

　　\(\overline{a+\mathrm{\,j}b}=a-\mathrm{\,j}b\)（式４）

と書きます。

実部を意味する \(\mathrm{Re}\)

複素数\( a + \mathrm{\,j}b \)から実部を取り出すときに\(\mathrm{Re}[　]\)を使います。

例えば、図２の \(3-\mathrm{\,j}2\) の実部は3ですから、

　　\(\mathrm{Re}[3-\mathrm{\,j}2] = 3\)

となります。

虚部を意味する\(\mathrm{Im}\)

複素数\( a + \mathrm{\,j}b \)から虚部を取り出すときに\(\mathrm{Im[　]}\)を使います。

例えば、図２の\( 3-\mathrm{\,j}2 \)の虚部は-2ですから、

　　\(\mathrm{Im}[3-\mathrm{\,j}2] = -2\)

となります。注意してほしいのは、jは虚部に入らず、虚部は実数となることです。

（誤り！） \(\mathrm{Im}[3-\mathrm{\,j}2] = -\mathrm{\,j}2\)

虚部は実数です！

絶対値記号｜｜

絶対値記号は、数直線上の原点からの距離を表します。3の場合は原点0からの距離は3ですし、-4の場合は原点からの距離は4になります。これらを

　　\(|3| = 3\)

　　\(|-4| = 4\)

と表記します。xを実数とするとき、

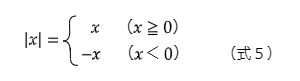
となります。

このことは複素数でも同様です。図２の複素数\( 3 – \mathrm{\,j}2\)の場合、原点からの距離は、３平方の定理から、\(\sqrt{3^2 + (-2)^2} = \sqrt{13}\)ですから、

　　\(|3-\mathrm{\,j}2| = \sqrt{13}\)

となります。

どの絶対値も、必ず | (数)| ≧ 0　が成立します。

不等号

実数の大小関係を表すのに用いられます。複素数は実部と虚部を持つため、そのものの大小比較はできません（絶対値の大小比較は可能）。

aはbを超える	\(a < b\)
aはb未満	\(a < b\)
aはb以上	\(a ≧ b\)
aはb以下	\(a ≦ b\)

充分大きい・充分小さい

aはbより充分大きい	\(a≫b\)
aはbより充分小さい	\(a≪b\)

ニアリーイコール「≒」のような曖昧そうな考え方かもしれませんが、必要な精度を計算するのに充分であれば、無視できるぐらい　大きい／小さいという判断ができれば怖くありません。

例えば、 内部抵抗\( 1\mathrm{\,Ω}\)、起電力\(1.5 \mathrm{\,V}\)の電池に \(1 \mathrm{\,kΩ}\)の抵抗をつなぐ場合に流れる電流を求めてみましょう。

まずは厳密な値をオームの法則で計算すれば、\(1 \mathrm{\,kΩ} = 1000 \mathrm{\,Ω}\)で、内部抵抗\(1 \mathrm{\,Ω}\)との直列合成抵抗は\(1000 \mathrm{\,Ω} + 1 \mathrm{\,Ω} = 1001 \mathrm{\,Ω}\)です。

流れる電流は\(\displaystyle \frac{1.5 \mathrm{\,V}}{ 1001 \mathrm{\,Ω}}=1.4985・・・ \mathrm{\,mA}\)となります。

一方、\(1000\mathrm{\,Ω}\)と\(1\mathrm{\,Ω}\)を比べると、\(1000\mathrm{\,Ω}≫1\mathrm{\,Ω}\)として \(1000\mathrm{\,Ω} + 1\mathrm{\,Ω} ≒ 1000\mathrm{\,Ω}\)として差し支えなさそうです。

1001円持っているときの所持金を約1000円として差し支えない感覚です。実際、この近似値で電流を計算すると \(\displaystyle \frac{1.5 \mathrm{\,V}}{ 1000\mathrm{\,Ω} }= 1.5 \mathrm{\,mA}\)となります。

厳密な計算と、\(1000\mathrm{\,Ω}≫1\mathrm{\,Ω}\)の計算を比較すれば、

　　厳密：\(1.4985・・・\mathrm{\,mA}\)

　　\(1000\mathrm{\,Ω}≫1\mathrm{\,Ω}\mathrm{\,：}1.5 \mathrm{\,mA}\)

となります。厳密な計算を有効数字５桁目（上記表示）で示すと差が現れますが、有効数字４桁の場合は\(1.499 \mathrm{\,mA}\)、３桁の場合は\(1.50 \mathrm{\,mA}\)となり、有効数字３桁では厳密に計算しても\(1000\mathrm{\,Ω}≫1\mathrm{\,Ω}\)としても答えは一致します。

このように、足し算・引き算をする際、計算結果に影響を与えないぐらい、無視できるような大きさに差が有るとき、「≪」や「≫」を用います。

無限大　∞

　充分大きな数の極限を∞と表記します。厳密にはいろんな取り決めをしないと行けないのですが、ざっくりとしたイメージはこのくらいで大丈夫です。

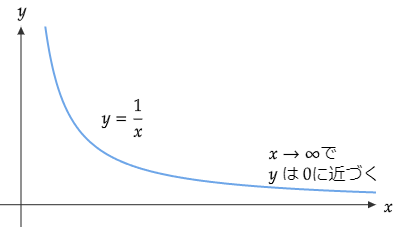
　図３の反比例のグラフ \(\displaystyle y = \frac{1}{x}\) で、\(x\) を大きくすると \(y\)はどんどん0 に近づいていきます。このとき、 \(x→∞\)　とすれば \(y→0\)となる、などと表記します。ざっくりと、雑に\(\displaystyle \frac{1}{∞} = 0 \)とする書籍もあります。

また、図４のグラフは、ＣＲ直列回路での充電電流の過渡現象の例です。

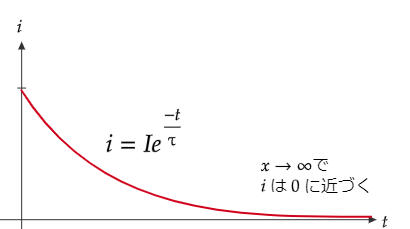
初期時刻\(t =0\)での充電電流\(I\)、時定数\(τ\)で、電流は

　　\(\displaystyle i(t) = I e^\frac{-t}{τ}\)

と変化します。このとき、\(t→∞\)とすれば、\(i(t)\)は0にどんどん近づきますから（∵指数関数の肩が負）、ざっくりと最終値・定常値を\(i(∞) = 0\) などと書きます。

比例　∝

\(I\)と\(V\)が比例関係にあるとき、\(I∝V\)と書きます。このとき、定数\(c\)によって

　　\(I = cV\)

あるいは別の定数 \(k\) によって

　　\(kI = V\)

とできます。

明らかに、\(\displaystyle k = \frac{1}{c}\)の関係がありますね。\(I\) が電流、\(V\)が電圧である場合、\(c\)はコンダクタンス（\(G \mathrm{\,[ S ]}\)）、kは抵抗（\(R \mathrm{\,[ Ω ]}\)）となります。

比　：

\(A:B\)　は、Aに対するBの比を表します。

　　\(A:B = C:D\)

のとき、

　　\(\displaystyle \frac{A}{B} = \frac{C}{D}\)

を意味します。両辺にBDをかければ、

　　\(AD = BD\)

と、元の式のたすきがけの形が得られます。

幾何学の記号

合同　≡

数の場合は同じであることを等号「＝」で表現しました。図形でも同じ記号を用いてもよいのですが、同じであることを示す対象が図形であることを明示するため、図形が同じであることは合同記号「≡」で示します。

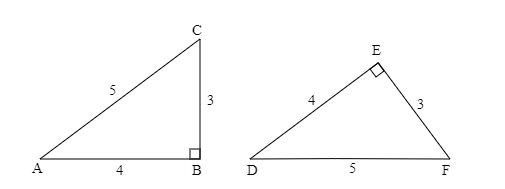
注意が必要なのは、図形は回転や平行移動をしてもよいという事です。図５に示された２つの直角三角形は合同で、対応する角を順に並べて

　\(\mathrm{\,△ABC}≡\mathrm{\,△DEF}\)

と表記します。

相似　∽

図形の各辺をそのまま定数倍して伸縮したとき、重なる図形があれば、その関係は相似であるといえます。図６の２つの直角三角形は、△ABCの各辺の長さを２倍すれば△DEFになることから、

　　\(\mathrm{\,△ABC}\mathrm{\,∽}\mathrm{\,△DEF}\)

と表記します。

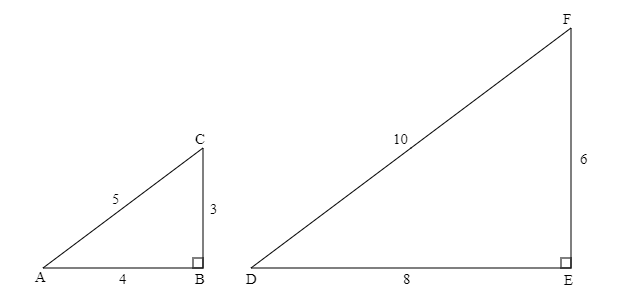
相似と比例には同値の関係があります。図６の２つの直角三角形で、

　　\(\mathrm{\,AB:BC:CA = DE:EF:FD}\)

が成立するからです。比が３つになっても扱いは同じで、すべて定数倍すれば一致するものがあるということです。図６の場合は

　　\(\mathrm{\,2 AB = DE}\)

　　\(\mathrm{\,2 BC = EF}\)

　　\(\mathrm{\,2 CA = FD}\)

となります。もちろん、これら３つの関係のうちから２つを取り出して、

　　\(\mathrm{\,AB:BC = DE:EF}\)

　　\(\mathrm{\,AB:CA = DE:FD}\)

　　\(\mathrm{\,BC:CA = EF:FD}\)

の関係だけ利用しても大丈夫です。

垂直　⊥　と　平行　//

２つの直線や線分のなす角が直角である場合には⊥を、平行である場合は//を用います。

　　\(\dot{V}\) と \(\dot{I}\) が直交　←→　\(\dot{V} ⊥ \dot{I}\)

　　\(\dot{V}\) と \(\dot{I}\) が平行　←→　\(\dot{V} // \dot{I}\)

と書けますが、ハッキリ位相関係を

　　\(\dot{V}\) が\(\dot{I}\) より90°進み　←→　\(\dot{V} = j X \dot{I}\)

　　\(\dot{V}\) と \(\dot{I}\) が同相　←→　\(\dot{V} = R\dot{I}\)

とする表記に慣れたほうがよいでしょう。

まとめ

この記事では、数学記号について解説しました。

記事内で紹介しきれなかった数学記号はたくさんありますが、まずはこれらの数学記号とその意味について知っておくことが、電気に関する様々な資格試験を受験する際に役立つはずです。

もし、電験三種の受験を検討していて、基礎的な学力に不安がある方には、オーム社オンラインスクールの「基礎力養成コース　電験三種」シリーズがおすすめです。

科目別に基礎から丁寧に解説する「理論」「電力」「機械」「法規」や、計算力の養成に特化した「電気数学」など、さまざまなプランをご用意しています。 ぜひ、受講をご検討ください！