数学では、いろいろな概念を記述する際に記号を使って式を書き表します。このように、数学上に抽象化された概念を簡潔に表すための記号を「数学記号」と呼びます。
「数学記号」のうち、数学定数や特殊関数、一定の性質を持つ変数を表す記号として、ギリシャ文字が使われています。
電気工事士、電気主任技術者試験など、電気に関する資格試験を受ける場合、この「ギリシャ文字」が何を表すのかについて知っておく必要があります。
この記事では、ギリシャ文字とその意味、さらに電気工事士・電気主任技術者試験ではどのように問題が出題されるのかをご紹介します。
数学で使われるギリシャ文字とその意味
ギリシャ文字とは、ギリシャ語を書き表すための文字のことです。ギリシャ文字の歴史は古く、もともとは古代ギリシア人によって作られ、ラテン文字はギリシア文字を元に作られました。
ラテン文字は26文字あり、大文字と小文字を合わせると52文字になります。しかし、数学や電気工学の数式を記述するのに、52文字では全然足りないのです。そこで、ギリシャ文字も数学記号として量記号や単位記号などに用いられています。

大文字と小文字
表中の\(A\)や\(B\)のように、ギリシャ文字の大文字は、ラテン文字と同一のものもたくさんあります。このようなラテン文字と同一の記号を用いると、混同してしまいややこしいので、現代の理系の文章でラテン文字と同一のギリシャ文字の大文字を用いることはほとんどありません。
抵抗の温度係数\(\alpha\)
最初にご紹介するのは、角度・抵抗の温度係数を表す\(\alpha\)です。読み方は「Alpha アルファ」です。
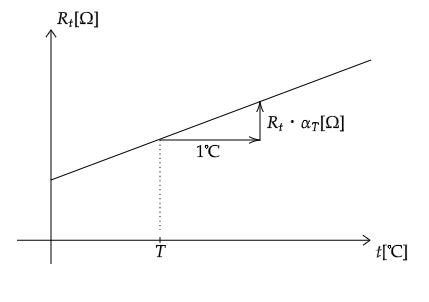
多くの場合、金属の抵抗値は、温度が上昇すると増加します。そこで、 金属ごとにその増加の割合を表すのが抵抗の温度係数です。下の表のように、常温における抵抗の温度係数が、各金属ごとによく調べられています。単位は\(\mathrm{\,[℃^{(-1)}]}\)です。
抵抗温度係数は温度によって異なります。\(T\mathrm{\,[℃]} \)における抵抗値を \(R_T \mathrm{\,[Ω]}\)とするとし、\(T\mathrm{\,[℃]} \)から 1℃上昇するときの抵抗温度係数を\(α_T \mathrm{\,[℃^{(-1)}]} \)とすれば、\( t\mathrm{\,[℃]}\)における抵抗値 \(R_t\mathrm{\,[℃]} \)は
\(R_t=R_t+{R_t}{\alpha_T}t=(1+{\alpha_T}t)R_T\)(式1)
と表されます。
| 名称 | \(\alpha\) \([10^{-3}/℃]\) |
|---|---|
| アルミニウム | 4.2 |
| 金 | 4.0 |
| 銀 | 4.1 |
| 水銀 | 0.99 |
| 錫 | 4.5 |
| 名称 | \(\alpha\) \([10^{-3}/℃]\) |
|---|---|
| タングステン | 5.3 |
| 鉄 | 6.6 |
| 軟鉄 | 4.3 |
| 鉛 | 4.2 |
| 白金 | 3.9 |
電気に関する資格試験では、電気工事士の場合、温度が変化した場合における抵抗値の変化を求めるような問題で出題されます。電験では、温度が変化することによる損失の変化や電気特性の変化まで問われることもあります。
ちなみにですが、金属の多くでは抵抗温度係数は正となります。つまり、温度が上昇すると抵抗値は増加します。一方、半導体材料の場合、抵抗温度係数は負になります。つまり、温度が上昇すると抵抗値は減少します。
角度の\(\alpha\)・\(\beta\)・\(\gamma\)・\(δ\)
ラテン文字だとa・b・c・dの順に対応するような文字です。数学や物理学の分野でしたら定数や係数に割り当てられることもありますが、電気関係の分野では角度に割り当てられることが多いです。また、交流回路をフェーザ(ベクトル)で表す場合、位相角は角度となりますから、これらの文字がフェーザの偏角を表されることもあります。
誘電正接で登場する損失角の\(δ\)
コンデンサの漏れ電流により生じる損失の度合いを表すために、図2の回路図を考えます。
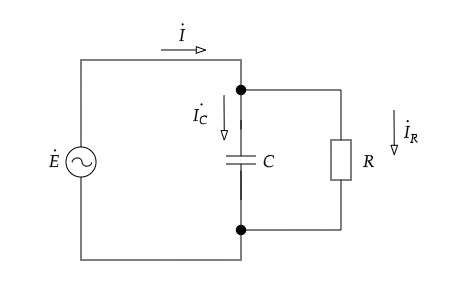
静電容量\(C\)に並列に漏れ電流が流れる抵抗\(R\)が接続されています。このときベクトル図は図3のようになります。
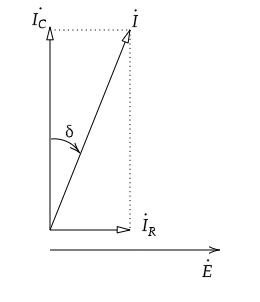
漏れ電流が無ければ、起電力 \(\dot{E}\)と電流\(\dot{I}\)は90°の位相差があり、損失は起こりません。ところが、漏れ電流\(\dot{ I_R}\)により、\(\dot{EI_R}\)\(\mathrm{\,[W]}\)の損失が生じます。このとき損失の起こりやすさを、図3の角度\(δ\)で表現し、この角度を損失角といいます。
実際、コンデンサの損失の度合いを表すときは、損失角\(δ\)そのものではなく、その正接(\(\tan\))をとった
\(\displaystyle \tanδ=\frac{I_R}{I_C}=ωCR\)(式2)
が用いられます。この\(\tan{δ}\)を誘電正接といいます。\(\tan{δ}\)が大きいほど、漏れ電流が大きく、損失の大きいコンデンサといえます。
負荷角・内部相差角・相差角の\(δ\)
同期発電機の誘導起電力と端子電圧の位相差を負荷角や内部相差角といい、\(δ\)で表します。また、送電線においても、送電端と受電端の電圧の位相差を相差角といい、\(δ\)で表します。図4は、三相同期発電機や送電線のモデルとして良く用いられる1相分の等価回路です。このベクトル図は図5のようになります。
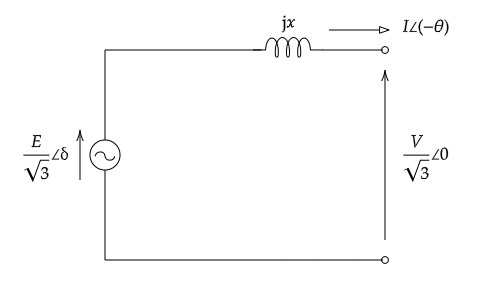
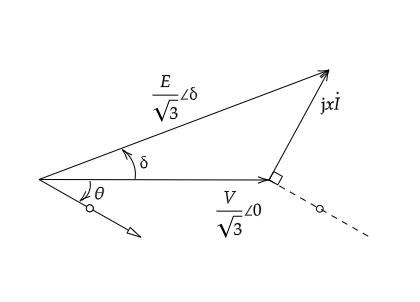
このときの3相分出力は
\(\displaystyle P=3\frac{V}{\sqrt{3}}I\cos\theta\)(式3)
となりますが、図5のベクトル図より、
\(\displaystyle P=\frac{VE}{x}\sin δ \)(式4)
が得られます。電験三種では必須の知識ですから、参考書等でチェックしておきましょう。
\(α・β\)が角度として用いられることは多いですが、\(γ\)まで登場することはまれではあります。ところが、後述の「\(Δ\)」と同様、\(δ\)には「微小」という意味も含蓄していることから、損失角や負荷角にもあてられているようです。
また、ここでの解説は割愛しますが、電験一種・二種の2次試験における機械・制御科目では、自動制御の中でデルタ関数\(δ(t)\)の知識が必要になります。そして、\(γ\)は数学のオイラー定数として用いられますが、電験で登場することはありません。
まれに\(γ\)が電気伝導率として利用されることもありますが、電気工学関係では\(σ\)が使われることが多いように感じます。
帰還率の\(β\)
機械科目の自動制御において、フィードバックの帰還率を表すのに\(β\)がよくあてられます。また、トランジスタやオペアンプの負帰還回路においても同様に、帰還率を表すのに用いられます。
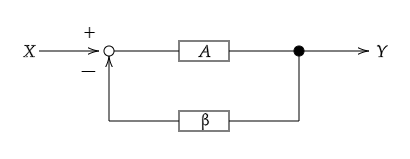
図6のように、増幅率\(A\)の増幅器に、\(β\)の帰還率でフィードバックを行うとき、伝達関数は
\(\displaystyle G=\frac{Y}{X} = \frac{A}{1+\beta A} \)(式5)
となります。
誘電率の\(ε\)
誘電率は「分極のしやすさ」を示す定数で、物質により様々な値をとります。興味深いのは、真空であっても誘電率の値があることです。真空中の誘電率は\(ε_0\)と表し、
\(ε_0 ≒ 8.8541878128×10^{-12} \mathrm{\,[F/m]}\)
です。
自然対数の底(ネイピア数)\(ε\)
数学の分野では、自然対数の底(ネイピア数)を\(e\) と表記します。しかし、電気工学関係の書籍の場合、起電力の量記号と被るのを避けるため、対応するギリシャ文字の\(ε\)を利用することがあります。
数学的な定義は、
\(ε=\displaystyle \lim_{ n \to \infty }{\left( 1+\frac{1}{n} \right) }\)(式6)
で、この極限は一定値に収束し、
\(ε=2.718281828459045235360287471352 ・・・\) (式7)
という無理数になることが知られています。
円周率\(π\)と同じくらい重要な数学定数で、自然界の法則にもたくさん現れます。電験三種までで登場する式としては、
・過渡現象
・オイラーの公式
があげられます。
電圧変動率の\(ε\)
変圧器や送電線路の電圧変動率に\(ε\)が利用されます。無負荷での電圧を\(V_0\)、定格や基準となる電圧を\(V_n\)とするとき、電圧変動率は
\(\displaystyle ε=\frac{V_n-V_o}{V_n}×100\mathrm{\,[%]}\)(式7)
で定義されます。電験三種の電力科目でも機械科目でも登場するもので、対象とする機器によって、電圧変動率を表記する様々な公式が得られます。
変化量・微少量の\(Δ\)
変化量や微少量を表現するのに、量記号に\(Δ\)を付記して使用します。例えば、時刻が\(t = 1 \mathrm{\,[s]}\)から\( t = 3 \mathrm{\,[s]}\)まで変化した時、時間の変化量は
\(Δt = 3 – 1 = 2 \mathrm{\,[s]}\)
などと表現します。
また、変化量が微小である(数学では0の極限操作ができるものを対象として微分という操作を行います)ときも\(Δ\)を付記します。例えば、ファラデーの電磁誘導に関する法則では、磁束の変化\(ΔΦ [Wb]\)、時刻の変化\(Δt [s]\)、巻数\(N\)のコイルの誘導起電力 \(e [V]\)を
\(\displaystyle e = – N \frac{ΔΦ}{Δt}\)
と表現します。
電験の試験においては、これらの変化量をグラフから求めたり、磁束変化を速度で表現したりする際に登場します。
行列式の\(Δ\)
連立方程式を解く際、クラメールの公式で同じ行列式が何度も登場します。行列式のDeterminantの頭文字Dがギリシャ文字Δに対応するため、時々置き換えられたりします。ただ、電験三種の問題はクラメールの公式を利用しなくても解くことができますので、掲載される参考書も少なくなっています。
\(Δ\)結線
数式ではないのですが、三相交流の起電力や負荷の結線方式で\(Δ\)結線が登場します。これは、結線の見た目が\(Δ\)の形そのものだからです。
減衰係数の\(ζ\)
振動現象において、力学の場合は摩擦力、電気回路系においては電気抵抗で、振動が減衰する程度を表す量です。自動制御の場合は2次遅系と呼ばれるシステムで登場します。図7は、ばねを様々な抵抗(制動・ブレーキ)の大きさの中で振動・減衰させている様子です。この図から、減衰係数ζが大きいほど、抵抗が大きいというざっくりとしたイメージをつかめるとよいでしょう。
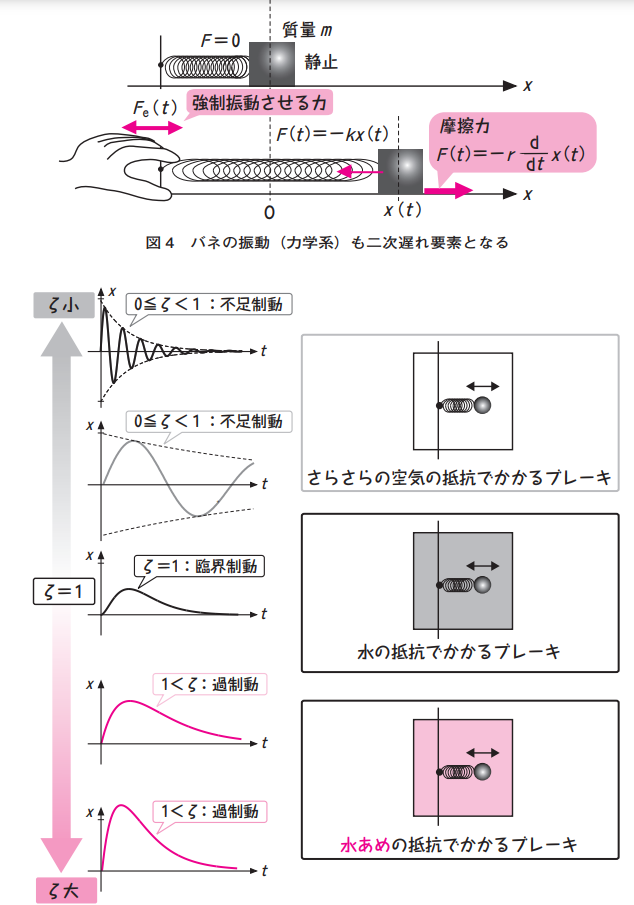
効率の\(η\)
電気の試験では様々な機器が登場しますが、様々なエネルギーを変換する装置が登場します。、例えば発電機は運動エネルギーを電気エネルギーに変換しますし、変圧器は電気エネルギーを異なる電圧の電気エネルギーに変換します。
このとき、全てのエネルギーが変換されるわけではなく、一部が損失として失われます。つまり、入力した分、一部がロスとなり、出力されます。このときの入力に対する出力の割合を効率といい、ギリシャ文字の\(η\)を用いて(式9)で定義されます。
\(\displaystyle η=\frac{\boldsymbol{(出力)}}{\boldsymbol{(入力)}}×100\mathrm{\,[%]}\)(式9)
(式9)のように、入力と出力を直接測定して算出した効率を実測効率といいます。しかし、効率の非常に高い装置として、例えば変圧器があります。この場合、入力と出力の値が非常に近く、測定器の精度では入力値と出力値がほぼ同一になることがあります。
例:入力電力 \(120 \mathrm{\,kW}\) 出力電力 \(120 \mathrm{\,kW}\) ?(←より高い精度で測れば \(119.2 \mathrm{\,kW})\)
→ \(\displaystyle η=\frac{120 \mathrm{\,kW}}{120 \mathrm{\,kW} }×100\mathrm{\,[%]}\)
そこで、(出力)=(入力)ー(損失) という関係を利用し、損失を測定することで
\(\displaystyle η=\frac{\boldsymbol{(入力 – 損失)}}{\boldsymbol{(入力)}}×100\mathrm{\,[%]}\)(式10)
と算出した効率を規約効率といいます。規約効率を用いることで、入力と損失を、別の測定レンジの計器を用いることができ、変圧器のような入力と出力が近い値をとる機器であっても、効率の測定がやりやすくなります。
例:入力 \(120 \mathrm{\,kW}\) 損失 \(800 \mathrm{\,W}\)(損失は、入力より小さいレンジの電力計で測定できる)
→ \(\displaystyle η =\frac{ (120 \mathrm{\,kW} – 0.8 \mathrm{\,kW})} {120 \mathrm{\,kW}}×100 = 99.3\mathrm{\,[%]}\)
角度の\(θ\)
角度は\(θ\)を用いて表されます。交流回路では、位相角としてもよく利用されます。
角度の単位には、1周を360°と表記する度数法と1周を\(2π\)と表記する弧度法があります。
温度の\(θ・Θ\)
英語のthermal (温度の)はギリシャ語でθερμοςと表記されることから、温度にも\(θ・Θ\)が用いられます。温度の単位は、セルシウス温度[℃]と絶対温度[K]があります。電気工学の教科書では、抵抗温度係数を計算する時には温度として \(θt\) や\( T\)を用いられることが多く、熱抵抗の計算の際には\(θ\)や\(Θ\)を用いることが多いように感じます。
\(ι\)
電気工学関係で用いられることはありません。
電気導電率の\(κ\)
電気導電率としては、後述の\(σ\)が用いられることが多いですが、中には\(κ\)を用いるテキストもあります。電気工学関連の書籍ではあまりありませんが、熱伝導率と電気導電率を同時に説明する際、両者を区別する時に、熱伝導率を\(κ\)、電気導電率を\(σ\)とすることがあります。
波長の\(λ・Λ\)
機械科目で照明を学ぶときに光の波長を表すのに\(λ・Λ\)が用いられます。大文字\(Λ\)が用いられることはあまりありません。ほんとうは、「長さ」を意味する英語の“length’’が使いたかったのでしょうけれど、他の長さや整数を表記するのにも使われますから、重複を避けるために対応するギリシャ文字を充てたのだと思います。
後述する光の振動数\(ν\mathrm{\,[Hz]}\)と光束\( c\mathrm{\,[m/s]}\)との間に、
\(c = νλ\) (式11)
の関係があります。
透磁率の\(μ\)
透磁率は、磁化の起こりやすさを表す値です。誘電率と同様、真空中にも誘電率の値があることが興味深いですね。真空中の透磁率は
\(μ_0 = 4π×10^{-7} \mathrm{\,[H/m]}\)
です。
真空中の誘電率\(ε_0 \mathrm{\,[F/m]}\)、真空中の透磁率\(μ_0\mathrm{\,[H/m]}\)、真空中の光速\(c \mathrm{\,[m/s]}\)との間には、
\(\displaystyle C=\frac{1}{\sqrt{ε_0 μ_0}}\)(式12)
の関係があります。マクスウェルが電磁気の法則から電磁波が(式12)の速度で伝播することを予言し、ヘルツが実験で示しました。
変数の\(Ξ・ξ\)
数学の変数として\(x, y, z\)の3組がよく利用されます。これと対を成す変数がほしいとき、\(a, b, c\)では定数に見えてしまいますね。そこで利用されるのが\(ξ, η, ζ\)です。電気関係の書籍でも使ってもよいのですが、この\(ξ・Ξ\)が書きにくいからか、あまり用いられていません。電気関係の書籍はおろか、数学や物理の入門書でも見かけなくなってきた気がします。
筆者が学生の頃、大学の先生が、「理系の学生になったんだったら\(ξ, η, ζ\)はかけなきゃ」と関西生まれの筆者には耳に残る関東の言葉で話されていたことを思い出します。もうその先生も鬼籍に入られましたが。
円周率の\(π\)
おそらく、日本の学校で最初に学ぶギリシャ文字が円周率の\(π\)ではないでしょうか。その由来は、「周囲」を意味する英語“perimeter’’のギリシャ語“περιμετρoζ’’ に由来するそうです。
円周率に関する話題は、その桁数のように尽きませんから、世界で一番美しい式と呼ばれる「オイラーの等式」を紹介します。
\({ε^{\mathrm{\,j}π}}+1=0\) (式13)
円周率\(π\)、自然対数の底\(ε\)、虚数単位\(\mathrm{\,j}= \sqrt{-1}\)、足し算の出発(元)となる0、掛け算の出発1の関係が1つの式に入っています。
相乗の\(Π\)
すべての変数を掛け算する操作を相乗といい、\(Π\)という記号で表します。例えば、
\(\displaystyle x_1=2,x_2=3,x_3=-1,x_4=\frac{1}{2}\)のとき
\(\displaystyle \prod_{i=1}^4 x_n = x_1・x_2・x_3・x_4\)
\(\displaystyle = 2×3×(-1)×\frac{1}{2}\)
\(=3\) (式14)
とします。電気工事士や電験の問題で現れることはありませんが、自分の計算メモなどを書くときなどに便利かもしれませんね。
総和の\(Σ\)
すべての変数を足し算する操作を総和といい、\(Σ\)という記号で表します。例えば、
\(\displaystyle \sum_{ n = 1 }^{ 4 }x_n=x_1+x_2+x_3+x_4\)
\(\displaystyle=2+3+(-1)+\frac{1}{2}\)
\(\displaystyle =\frac{9}{2}\) (式15)
とします。
電験の参考書によっては、\(Σ\)記号の上下に示す添え字の範囲を省略して、その添え字すべての和を表す場合があります。
例えば、\(YーΔ\)変換の公式などで、3つの抵抗\(R_1, R_2, R_3\)の和を
\(ΣR=R_1+R_2+R_3\) (式16)
などとする場合があります。
電気導電率の\(σ\)
電気導電率には\(σ\)が用いられることが一般的です。前述のように、\(γ\)や\(κ\)が用いられることがまれにあります。なお、電気「伝導」率も電気導電率同じ意味で用いられます。物理学の本では伝導率とすることが、電気工学では導電率とすることが多いです。
振動数の\(ν\)
交流電源の周波数はfrequency(周波数)の\(f \mathrm{\,[Hz]}\)が用いられますが、光の振動数の場合は\(ν\mathrm{\,[Hz]}\)が用いられます。おそらくですが、振動の数としてnumberの\(n\)を使いたかったのかもしれません。ギリシャ文字の\(ν\)はラテン文字の\(n\)に対応しますから、こちらが充てられたのでしょう。
時定数の\(τ\)
過渡現象が起こる時間の目安として時定数が用いられます。過渡現象を表す式で、指数関数(底は自然対数)の肩が-1となるときの時刻が時定数の値です。CR直列回路では\(τ= CR\mathrm{\, [s]}\)、RL直列回路では\(\displaystyle τ= \frac{L}{R}\mathrm{\, [s]}\)です。
時定数は小文字の\(t\)や大文字の\(T\)に添え字をつけて表されることもあります。ただ、時刻に\(t\)が、周期に\(T\)が用いられますから、重複を避けるためにギリシャ文字が用いられる書籍も多いです。
トルクの\(τ\)
機械科目で、回転機のトルク\(\mathrm{\,[N・m]}\)を表すのに\(τ\)が用いられることがあります。トルクは\(T\)が充てられることもよくありますが、周期等の時間を表す\(T\)と重複してしまうときは、ギリシャ文字で回避されることもあります。
\(υ\)
電気関係で用いられることはありません。
磁束の\(Φ・φ\)
磁束\(\mathrm{\,[W]}\)を表すのに\(Φ・φ\)が用いられます。時間変化しない一定値を大文字で、時間変化する量を小文字で表す場合は、それぞれ\(Φ\)と\(φ\)が用いられます。
角度の\(φ\)
\(φ\)は磁束を表すだけでなく、角度を表すのにも用いられます。例えば、瞬時値が
\(v = \sqrt{2} V \sin (ωt + θ)\)
と表される電圧の位相を\(φ = ωt + θ\) と表し、\(θ\)の初期位相と区別して
\(v =\sqrt{2} V \sin φ\)
と表記する時などに用いると便利です。
なお、フォント(書体)としては「\(\phi\)」と「\(\varphi\)」があります。文字コードが同じですので、コンピュータ上ではフォントの違いでしかないのですが、数式上では別の文字として扱われることがほとんどですので注意しましょう。
直径の\(φ\)
ネジや電線、穴等の直径を示すのに\(φ\)が使われることがあります。電気工事士の勉強をしていると、直径19 mmの金属電線管はE19と表記されます。この直径は\(φ19\) と示されることもあります。
電気感受率の\(χ\)
誘電率\(ε\)と同様、分極の起こりやすさを表す量ですが、電気工事士や電験の試験で現れることはありません。
電束の\(Ψ・ψ\)
電束は、電荷と同様の単位\(\mathrm{\,[C]}\)を持つため、電荷と同じ\(Q\mathrm{\,[C]}\)が使われることがあります。しかし、電荷そのものの値と、電束を区別したいときは、\(Ψ・ψ\)が用いられることがあります。
電束についての解説は、新電気2024年8月号『電磁気のこころ』第1回 「電界\(E\)と電束密度\(D\)の違い」が秀逸でオススメです。
角度の\(ψ\)
\(φ\)と同様に、\(ψ\)を角度に用いることもできますが、電気関係で登場する頻度は少ないです。
角速度・角周波数の\(ω・Ω\)
角速度・角周波数には\(ω \mathrm{\,[rad/s]}\)が用いられます。角周波数に大文字の\(Ω\)を用いてもよいのですが、後述のオーム社さんの社名でもある電気抵抗の\(\mathrm{\,Ω}\)(オーム)が圧倒的に頻出ですから、電気関係で\(Ω\)が角周波数になることはほぼありません。
電気抵抗の\(\mathrm{\,Ω}\)
電気を勉強すると初めの方で習うこの読み方、「オーム」です。でも、元はギリシャ文字の「オメガ」の大文字です。偉大なオーム先生 (Ohm) の頭文字はOですが、ゼロと区別するのが難しいため、発音の似たギリシャ文字Ωが充てられたそうです。オーム社さんの創業者も、扇本眞吉氏(O)[電機学校創設者]、廣田精一氏(H)[電機学校創設者・オーム社初代代表者]、丸山莠三氏(M)[当時の電機学校教頭]と、頭文字がOHMとのこと、すごいご縁と感じます。
まとめ
この記事では、数学で用いられるギリシャ文字について解説しました。
これらのギリシャ文字とその意味について知っておくことで、電気に関する様々な資格試験を受験する際に役立つはずです。
もし、電験三種の受験を検討していて、基礎的な学力に不安がある方には、オーム社オンラインスクールの「基礎力養成コース 電験三種」シリーズがおすすめです。
科目別に基礎から丁寧に解説する「理論」「電力」「機械」「法規」や、計算力の養成に特化した「電気数学」など、さまざまなプランをご用意しています。
ぜひ、受講をご検討ください。
この記事を書いた人

山下 明
1991年大阪府出身。高校在学中に電験三種試験に合格。大阪市立大学工学部(電子・物理工学科)在学中に、工業高校で使用される「電気基礎」の教科書を発行。1947年に教科書検定制度が開始されて以降、大学生が個人で文部科学省検定済教科書を発行するのは初めてのことであり、大きな話題となった。
大学卒業後は大阪府内の工科高校に勤務ののち、執筆・講師活動へ入る。月刊誌「新電気」で2014年より「やさしく語る電気のイメージ 電気理論の入門講座」を連載開始(現在は「やさしく語る電気のイメージ 電気機器の入門講座」を連載中)、企業への出張講習も行うなど多忙な日々を送っている。

オーム社オンラインスクールについて
創業 大正14年の理工系専門出版社オーム社が発行している各種資格試験書籍のうち、読者の皆様から特に好評をいただいている書籍をベースにした講義動画を配信。
講義では過去の試験問題を分析し、広範な出題分野から重要なポイントのみ厳選していますので、効率的に学習し、最短で合格することが可能です。
インターネットに接続できる環境があれば、24時間いつでも動画を視聴することができます。また、PC以外にもタブレットやスマートフォンなどの機器でも視聴可能ですので、通学・通勤中や移動時間など、すきま時間を活用していつでもどこでも学習をすすめることができます。